目录
- 第一门课:第二门课 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
- 1.9 归一化输入(Normalizing inputs)
- 1.10 梯度消失/梯度爆炸(Vanishing / Exploding gradients)
第一门课:第二门课 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
1.9 归一化输入(Normalizing inputs)
训练神经网络,其中一个加速训练的方法就是归一化输入。假设一个训练集有两个特征,输入特征为 2 维,归一化需要两个步骤:
1.零均值
2.归一化方差;
我们希望无论是训练集和测试集都是通过相同的μ和
σ
2
σ^2
σ2定义的数据转换,这两个是由训练集得出来的。

第一步是零均值化, μ = 1 m ∑ i = 1 m x ( i ) μ=\frac{1}{m}\sum_{i=1}^m{x^{(i)}} μ=m1∑i=1mx(i),它是一个向量,𝑥等于每个训练数据 𝑥减去𝜇,意思是移动训练集,直到它完成零均值化
第二步是归一化方差,注意特征 x 1 x_1 x1的方差比特征 x 2 x_2 x2的方差要大得多,我们要做的是给𝜎赋值, σ 2 = 1 m ∑ i = 1 m ( x ( i ) ) 2 σ^2 =\frac{1}{m}\sum_{i=1}^m{(x^{(i)})^2} σ2=m1∑i=1m(x(i))2 ,这是节点y 的平方, σ 2 σ^2 σ2是一个向量,它的每个特征都有方差,注意,我们已经完成零值均化, ( x ( i ) ) 2 {(x^{(i)})^2} (x(i))2元素 y 2 y^2 y2就是方差,我们把所有数据除以向量 σ 2 σ^2 σ2,最后变成上图形式。
x_1和x_2的方差都等于 1。提示一下,如果你用它来调整训练数据,那么用相同的 μ和 σ 2 σ^2 σ2来归一化测试集。尤其是,你不希望训练集和测试集的归一化有所不同,不论μ的值是什么,也不论 σ 2 σ^2 σ2的值是什么,这两个公式中都会用到它们。所以你要用同样的方法调整测试集,而不是在训练集和测试集上分别预估μ和 σ 2 σ^2 σ2。因为我们希望不论是训练数据还是测试数据,都是通过相同 μ 和𝜎2定义的相同数据转换,其中 μ和 σ 2 σ^2 σ2是由训练集数据计算得来的。
我们为什么要这么做呢?为什么我们想要归一化输入特征,回想一下右上角所定义的代价函数。
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
(
i
)
,
y
(
i
)
)
J(w,b) =\frac{1}{m}\sum_{i=1}^m{L(\hat{y}^{(i)},y^{(i)})}
J(w,b)=m1i=1∑mL(y^(i),y(i))
如果你使用非归一化的输入特征,代价函数会像这样:
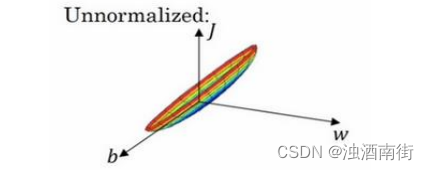
这是一个非常细长狭窄的代价函数,你要找的最小值应该在这里。但如果特征值在不同范围,假如𝑥1取值范围从 1 到 1000,特征𝑥2的取值范围从 0 到 1,结果是参数𝑤1和𝑤2值的范围或比率将会非常不同,这些数据轴应该是𝑤1和𝑤2,但直观理解,我标记为𝑤和𝑏,代价函数就有点像狭长的碗一样,如果你能画出该函数的部分轮廓,它会是这样一个狭长的函数。
然而如果你归一化特征,代价函数平均起来看更对称,如果你在上图这样的代价函数上运行梯度下降法,你必须使用一个非常小的学习率。因为如果是在这个位置,梯度下降法可能需要多次迭代过程,直到最后找到最小值。但如果函数是一个更圆的球形轮廓,那么不论从哪个位置开始,梯度下降法都能够更直接地找到最小值,你可以在梯度下降法中使用较大步长,而不需要像在左图中那样反复执行。
当然,实际上𝑤是一个高维向量,因此用二维绘制𝑤并不能正确地传达并直观理解,但总地直观理解是代价函数会更圆一些,而且更容易优化,前提是特征都在相似范围内,而不是从 1 到 1000,0 到 1 的范围,而是在-1 到 1 范围内或相似偏差,这使得代价函数𝐽优化起来更简单快速。
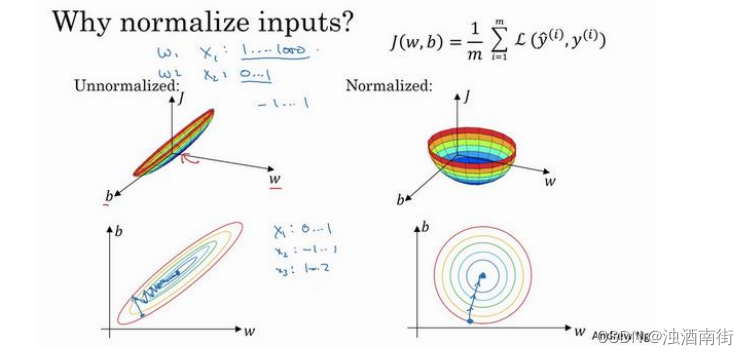
实际上如果假设特征𝑥1范围在 0-1 之间,𝑥2的范围在-1 到 1 之间,𝑥3范围在 1-2 之间,它们是相似范围,所以会表现得很好。
当它们在非常不同的取值范围内,如其中一个从 1 到 1000,另一个从 0 到 1,这对优化算法非常不利。但是仅将它们设置为均化零值,假设方差为 1,就像上一张幻灯片里设定的那样,确保所有特征都在相似范围内,通常可以帮助学习算法运行得更快。
所以如果输入特征处于不同范围内,可能有些特征值从 0 到 1,有些从 1 到 1000,那么归一化特征值就非常重要了。如果特征值处于相似范围内,那么归一化就不是很重要了。执行这类归一化并不会产生什么危害,我通常会做归一化处理,虽然我不确定它能否提高训练或算法速度。
这就是归一化特征输入,下节课我们将继续讨论提升神经网络训练速度的方法。
1.10 梯度消失/梯度爆炸(Vanishing / Exploding gradients)
训练神经网络,尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸,也就是你训练神经网络的时候,导数或坡度有时会变得非常大,或者非常小,甚至于以指数方式变小,这加大了训练的难度。
这节课,你将会了解梯度消失或梯度爆炸的真正含义,以及如何更明智地选择随机初始化权重,从而避免这个问题。 假设你正在训练这样一个极深的神经网络,为了节约幻灯片上的空间,我画的神经网络每层只有两个隐藏单元,但它可能含有更多,但这个神经网络会有参数
W
[
1
]
,
W
[
2
]
,
W
[
3
]
W^{[1]},W^{[2]},W^{[3]}
W[1],W[2],W[3]等等,直到
W
[
l
]
W^{[l]}
W[l],为了简单起见,假设我们使用激活函数
g
(
z
)
=
z
g(z) = z
g(z)=z,也就是线性激活函数,我们忽略𝑏,假设
b
[
l
]
=
0
b[l]=0
b[l]=0,如果那样的话,输出:
y
=
W
[
L
]
W
[
L
−
1
]
W
[
L
−
2
]
…
W
[
3
]
W
[
2
]
W
[
1
]
x
y = W^{[L]}W^{[L−1]}W^{[L−2]} … W^{[3]}W^{[2]}W^{[1]}x
y=W[L]W[L−1]W[L−2]…W[3]W[2]W[1]x
如果你想考验我的数学水平,
W
[
1
]
x
=
z
[
1
]
W^{[1]}x = z^{[1]}
W[1]x=z[1],因为b = 0,所以我想
z
[
1
]
=
W
[
1
]
x
,
a
[
1
]
=
g
(
z
[
1
]
)
z^{[1]} = W^{[1]}x,a^{[1]} =g(z^{[1]})
z[1]=W[1]x,a[1]=g(z[1]),因为我们使用了一个线性激活函数,它等于
z
[
1
]
z^{[1]}
z[1],所以第一项
W
[
1
]
x
=
a
[
1
]
W^{[1]}x = a^{[1]}
W[1]x=a[1],通过推理,你会得出
W
[
2
]
W
[
1
]
x
=
a
[
2
]
W^{[2]}W^{[1]}x = a^{[2]}
W[2]W[1]x=a[2],因为
a
[
2
]
=
g
(
z
[
2
]
)
a^{[2]} = g(z^{[2]})
a[2]=g(z[2]),还等于
g
(
W
[
2
]
a
[
1
]
)
g(W^{[2]}a^{[1]})
g(W[2]a[1]),可以用
W
[
1
]
x
W^{[1]}x
W[1]x替换
a
[
1
]
a^{[1]}
a[1],所以这一项就等于
a
[
2
]
a^{[2]}
a[2],这个就是
a
[
3
]
(
W
[
3
]
W
[
2
]
W
[
1
]
x
)
a^{[3]}(W^{[3]}W^{[2]}W^{[1]}x)
a[3](W[3]W[2]W[1]x)。
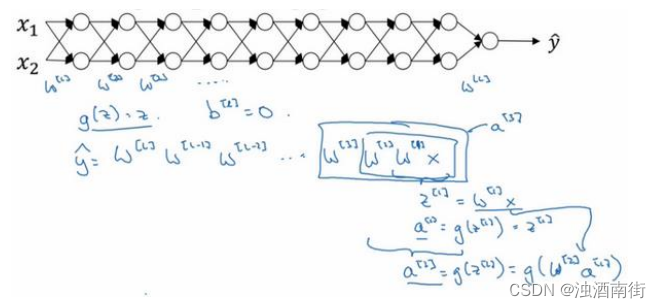
所有这些矩阵数据传递的协议将给出
y
^
\hat{y}
y^而不是𝑦的值。
假设每个权重矩阵 W [ L ] = [ 1.5 0 0 1.5 ] W^{[L]} =\begin{bmatrix}1.5 & 0 \\0 & 1.5 \end{bmatrix} W[L]=[1.5001.5],从技术上来讲,最后一项有不同维度,可能它就是余下的权重矩阵, y = W [ 1 ] [ 1.5 0 0 1.5 ] ( L − 1 ) x y= W^{[1]}\begin{bmatrix}1.5 & 0 \\0 & 1.5 \end{bmatrix}^{(L−1)}x y=W[1][1.5001.5](L−1)x,因为我们假设所有矩阵都等于它,它是 1.5倍的单位矩阵,最后的计算结果就是 y ^ \hat{y} y^, y ^ \hat{y} y^也就是等于 1. 5 ( L − 1 ) x 1.5^{(L−1)}x 1.5(L−1)x。如果对于一个深度神经网络来说𝐿值较大,那么 y ^ \hat{y} y^的值也会非常大,实际上它呈指数级增长的,它增长的比率是 1. 5 L 1.5^L 1.5L,因此对于一个深度神经网络,𝑦的值将爆炸式增长。
相反的,如果权重是 0.5, W [ L ] = [ 1.5 0 0 1.5 ] W^{[L]} =\begin{bmatrix}1.5 & 0 \\0 & 1.5 \end{bmatrix} W[L]=[1.5001.5],它比 1 小,这项也就变成了 0. 5 L 0.5^L 0.5L,矩阵 y = W [ 1 ] [ 0.5 0 0 0.5 ] ( L − 1 ) x y=W^{[1]}\begin{bmatrix}0.5 & 0 \\0 & 0.5 \end{bmatrix}^{(L−1)}x y=W[1][0.5000.5](L−1)x,再次忽略 W [ L ] W^{[L]} W[L],因此每个矩阵都小于 1,假设 x 1 x_1 x1和 x 2 x_2 x2都是 1,激活函数将变成 1 2 , 1 2 , 1 4 , 1 4 , 1 8 , 1 8 \frac{1}{2},\frac{1}{2},\frac{1}{4},\frac{1}{4},\frac{1}{8},\frac{1}{8} 21,21,41,41,81,81等,直到最后一项变成 1 2 L \frac{1}{2^L} 2L1,所以作为自定义函数,激活函数的值将以指数级下降,它是与网络层数数量𝐿相关的函数,在深度网络中,激活函数以指数级递减。我希望你得到的直观理解是,权重W只比 1 略大一点,或者说只是比单位矩阵大一点,深度神经网络的激活函数将爆炸式增长,如果W比 1 略小一点,可能是 [ 0.9 0 0 0.9 ] \begin{bmatrix}0.9 & 0 \\0 & 0.9\end{bmatrix} [0.9000.9]。
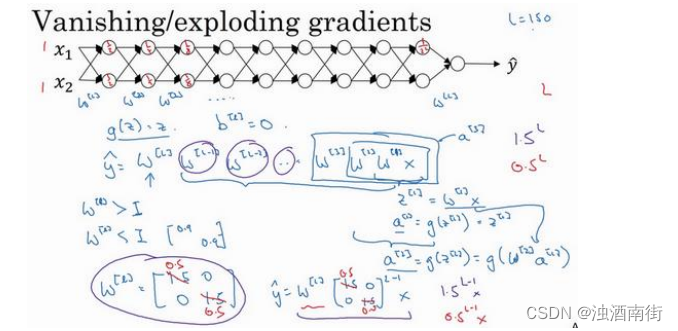
在深度神经网络中,激活函数将以指数级递减,虽然我只是讨论了激活函数以与𝐿相关的指数级数增长或下降,它也适用于与层数𝐿相关的导数或梯度函数,也是呈指数级增长或呈指数递减。
对于当前的神经网络,假设𝐿 = 150,最近 Microsoft 对 152 层神经网络的研究取得了很大进展,在这样一个深度神经网络中,如果激活函数或梯度函数以与𝐿相关的指数增长或递减,它们的值将会变得极大或极小,从而导致训练难度上升,尤其是梯度指数小于𝐿时,梯度下降算法的步长会非常非常小,梯度下降算法将花费很长时间来学习。
总结一下,我们讲了深度神经网络是如何产生梯度消失或爆炸问题的,实际上,在很长一段时间内,它曾是训练深度神经网络的阻力,虽然有一个不能彻底解决此问题的解决方案,但是已在如何选择初始化权重问题上提供了很多帮助。